Bab 1: Bilangan Berpangkat dan bentuk akar

A. Bilangan berpangkat
Pangkat suatu bilangan didefinisikan suatu perkalian bilangan secara berulang dengan bilangan itu sendiri
Demikian seterusnya sehingga diperoleh bentuk umum sebagai berikut.

Pangkat Bulat Negatif Pangkat Nol Bilangan Pecahan Berpangkat Bilangan Berpangkat Pecahan Sumber :http://uripambaripto.blogspot.co.id/2015/01/materi-bilangan-berpangkat-dan-bentuk.html Copy the BEST Traders and Make Money : http://bit.ly/fxzulu

Copy the BEST Traders and Make Money : http://bit.ly/fxzulu

B. Bentuk Akar
Bentuk akar adalah akar dari suatu bilangan yang hasilnya bukan bilangan Rasional.
Bentuk akar dapat disederhanakan menjadi perkalian dua buah akar pangkat bilangan dengan salah satu akar memenuhi definisi
√a² = a jika a ≥ 0, dan –a jika a < 0
Contoh :
Sederhanakan bentuk akar berikut √75
Jawab :
√75 = √25x3 = √25 x √3 = 5√3
C. Bilangan Berpangkat Rasional
Bilangan rasional adalah bilangan yang dapat dinyatakan dalam bentuk ^a/_b dengan a, b bilangan bulat dan b ≠ 0. Bilangan rasional merupakan gabungan dari bilangan bulat, nol, dan pecahan. Contoh bilangan rasional adalah -5,-1/2,0,3,3/4,dan 5/9

_{Bab 2: Pola ,Barisan,dan Deret}

_{- Pola bilangan dapat diartikan sebagai susunan bilangan yang memiliki keteraturan}
_{- Dalam matematika dikenal beberapa jenis pola, antara lain:}
_{1) Pola bilangan ganjil}
_{adalah: 1,3,5,7,9}
_{Rumus suku ke-n dari pola bilangan ganjil}
_{adalah 2n-1 dengan n anggota bilangan asli}
_{contoh: n =1, urutan ke-1 = 2(1)-1=1}
_{n = 2, urutan ke-2 = 2 (2)-1=3}
_{n = 3, urutan ke-3 = 2 (3)-1= 5}
_{2) Pola bilangan genap}
_{adalah 2,4,6,8...}
_{Rumus suku ke-n dari pola bilangan genap adalah 2n, dengan n anggota bilangan asli}
_{contoh: n=1, urutan ke-1 = 2 (1) = 2}
_{n=2, urutan ke-2 = 2 (2) = 4}
_{n=3, urutan ke-3 = 2 (3) = 6}
_{3) Pola bilangan segitiga}
_{adalah 1,3,6,10..}
_{Rumus urutan ke-n dari pola bilangan segitiga adalah n(n+1) = 1 dengan n anggota bilangan asli}
₂
_{Contoh: n=1, urutan ke-1= 1(1+1) =1}
₂
_{n=2, urutan ke-2 = 2(2+1) = 3}
₂
n=3 urutan ke-3 = 3(3+1) = 6
                                                  2
   4) Pola bilangan persegi
       adalah 1,4,9,16
       Rumus urutan ke-n dari pola bilangan persegi adalah nxn dengan anggota bilangan asli
       Contoh: Tuliskan pola bilangan persegi hingga suku ke-9
9x9=81
1,4,9,16,25,36,49,64,81
    5) Pola bilangan persegi panjang
adalah 2,6,12,20
Rumus urutan ke-n dari pola bilangan persegi panjang adalah n(n+1) dengan n anggota bil asli
        Contoh: n=1, urutan ke-1 = 1(1+1)=2
                     n=2, urutan ke-2= 2(2+1)=6
                     n=3, urutan ke-3 = 3(3+1)= 12
                    n = 4, urutan ke-4 = 4(4+1)=20
    6) Pola bilangan segitiga pascal
adalah sebagai berikut

Rumus jumlah bilangan dari baris, pada segitiga pascal adalah 2n-1 dengan n anggota bilangan asli

Pengertian Barisan bilangan

Jika bilangan –bilangan diurutkan dengan aturan tertentu ,maka akan diperoleh suatu barisan bilangan.Tiap-tiap bilangan yang terdapat pada barisan bilangan disebut suku dari barisan itu .Jika aturan suatu barisan telah diketahui, maka suku berikutnya dari barisan tersebut dapat ditentukan

Contoh :

1. 2, 6 , 10, 14,…

Aturan pembentukannya adalah “ ditambah 4”

Dua suku berikunya adalah 18 dan 22.

2. 1, 2, 5, 10,…

Aturan pembentukannya adalah “ ditambah bilangan ganjil berurutan “

Dua suku berikutnya adalah 17 dan 26

Barisan dan deret artimatika

barisan bilangan adalah urutan dari bilangan yang dibuat berdasarkan aturan tertentu. Sedangkan untuk barisan aritmatika adalah sebuah barisan bilangan dimana setiap pasangan suku-suku yang berurutan memiliki selisih yang sama. contoh : 6,9,12,15,…

Selisih bilangan pada barisan aritmatika disebut beda yang biasa disimbolkan dengan huruf b, untuk contoh diatas memiliki nilai beda 3. Dan bilangan yang menyusun suatu barisan disebut suku, dimana suku ke n dari suatu barisan disimbolkan dengan U_n sehingga untuk suku ke 5 dari suatu barisan biasa disebut dengan U₅. Khusus untuk suku pertama dari suatu barisan biasa disimbolkan dengan huruf a.

Yang dimaksud dengan deret aritmatika adalah penjumlahan dari semua anggota barisan aritmatika secara berurutan. Contoh dari deret aritmatika yaitu 7 + 10 + 13 + 16 + 19 + …

Rumus suku ke-n deret aritmatika atau barisan aritmatika adalah Un=U1+(n-1)b

SISIPAN DAN DERET ARITMATIKA

Sisipan pada deret aritmatika yaitu menambahkan beberapa buah bilangan diantara dua suku yang berurutan pada suatu deret aritmatika sehingga diperoleh deret aritmatika yang baru. Sebagai contoh :

Deret mula-mula = 4 + 13 + 22 + 31 +……

Setelah disisipi = 4 + 7 + 10 + 13 + 16 + 19 + 22 + 25 + 28 + 31 +……

Untuk beda dari deret baru ini biasanya dinyatakan dengan b1, dapat ditentukan dengan rumus berikut :

b1 = b/(k+1)

b1 = beda deret baru

b = beda deret mula-mula

k = banyak bilangan yang disisipkan

Suku tengah suatu deret aritmetika

Ut= U1+Un

Jumlah n suku pertama.Deret aritmetika

Sn=1/2n (U1+Un) atau Sn=1/2n(2U1+(n-1)b)

Deret Geometri

Jumlah dari n suku pertama suatu barisan geometri disebut sebagai deret geometri. Jika suku ke-n dari barisan geometri dirumuskan: a_n = a₁rⁿ^{– 1}, maka deret geometri dapat dituliskan sebagai,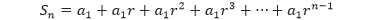

Jika kita mengalikan deret tersebut dengan –r kemudian menjumlahkannya dengan deret aslinya, kita mendapatkan
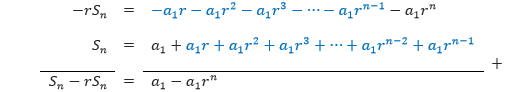
Sn - rSn

Sehingga kita memperoleh S_n – rS_n = a₁ – a₁rⁿ. Dengan menyelesaikan persamaan tersebut untuk S_n, kita mendapatkan
Menentukan Sn

Hasil di atas merupakan rumus jumlah n suku pertama dari barisan geometri.

Jumlah n Suku Pertama Barisan Geometri
Diberikan suatu barisan geometri dengan suku pertama a₁ dan rasio r, jumlah n suku pertamanya adalah

Atau bisa dikatakan: Jumlah dari barisan geometri sama dengan selisih dari suku pertama dan suku n + 1, kemudian dibagi dengan 1 dikurangi rasionya.

Bab 3 : Perbandingan Bertingkat

- Perbandingan adalah membandingkan 2 nilai atau lebih dari suatu besaran yang sejenis dan dinyatakan dengan cara sederhana
* Persentase
     lambang % dibaca "persen"
     Pecahan dengan penyebut sama dengan 100 disebut perseratus,atau persen
     contoh: 35/100 dibaca 35 persen dan dilambangkan 35%. Dalam kehidupan sehari-hari persentase sering digunakan dalam masalah aritmetika sosial,statistika,dan lain sebagainya
* Perbandingan senilai
     adalah perbandingan dua besaran,dimana jika satu besaran semakin besar maka besaran yang lain juga akan semakin besar,dan sebaliknya
* Perbandingan Berbalik nilai (harga)
     adalah perbandingan dua besaran dimana jika satu besaran semakin besar maka besaran yang lain akan semakin kecil dan sebaliknya.
- Masalah yang sering berkaitan dengan perbandingan berbalik nilai antara lain:
   1.) Banyak pekerja dengan waktu yang diperlukan untuk menyelesaikan pekerjaan (untuk pekerjaan yang sama)
   2.) Kecepatan dengan waktu tempuh (untuk jarak yang sama)

Persentase Untung Rugi

Untuk mencari persentasi untung/rugi, digunakan rumus-rumus berikut:
$\displaystyle \textup{Persentase untung}=\frac{\textup{untung}}{\textup{harga beli}}\times 100\%$
$\displaystyle \textup{Persentase rugi}=\frac{\textup{rugi}}{\textup{harga beli}}\times 100\%$
Contoh soal:
Contoh 1:
Pak Nasrul membeli sebuah sepeda yang harganya Rp 150.000,00 kemudian dijual kembali dengan harga Rp 168.000,00. Berapa persen (%) pak Nasrul mendapat untung?
Jawab:
harga beli = Rp 150.000,00
harga jual = Rp 168.000,00
untung = harga jual – harga beli
=168.000 – 150.000
=18.000
sehingga
$\displaystyle \textup{Persentase untung}=\frac{\textup{untung}}{\textup{harga beli}}\times 100\%$
$\displaystyle =\frac{18.000}{150.000}\times 100\%$
$\displaystyle =\frac{3}{25}\times 100\%$
$\displaystyle =12\%$
jadi pak Nasrul mendapatkan untung sebesar 12%.

TABUNGAN DAN BUNGA BANK

a. Rumus-rumus pada bunga harian

1. Bunga(Rp) = (Modal x waktu x bunga(%)) / (360x100)
2. Waktu = ( Bunga yang diterima(Rp) / Bunga dalam setahun(Rp) ) x 360
3. Modal = (Bunga(Rp) x 360 x 100 )/ Waktu x bunga(%)

b. Rumus pada Bunga Bulanan

1. Bunga (Rp) =( Modal x waktu x bunga(%) ) / (12 x 100)
2. Waktu ( bulan ) =(Bunga yang diterima / Bunga dalam setahun)x 12
3. Modal = (Bunga(Rp) x 12 x 100) / waktu bunga(%)

c. Rumus pada Bunga Tahunan

1. Bunga(Rp) =( Modal x Waktu x Bunga(%) ) / 100
2. Waktu (tahun) = Bunga yang diterima / Bunga dalam setahun
3. Modal =( Bunga(Rp) x 100 )/ (Waktu x Bunga(%) )

Bunga (dalam %) =(bunga setahun / modal) x 100%

TABUNGAN DAN BUNGA BANK

a. Rumus-rumus pada bunga harian
   1. Bunga(Rp) = (Modal x waktu x bunga(%)) / (360x100)
   2. Waktu = ( Bunga yang diterima(Rp) / Bunga dalam setahun(Rp) ) x 360
   3. Modal = (Bunga(Rp) x 360 x 100 )/ Waktu x bunga(%)
b. Rumus pada Bunga Bulanan
   1. Bunga (Rp) =( Modal x waktu x bunga(%) ) / (12 x 100)
   2. Waktu ( bulan ) =(Bunga yang diterima / Bunga dalam setahun)x 12
   3. Modal = (Bunga(Rp) x 12 x 100) / waktu bunga(%)
c. Rumus pada Bunga Tahunan
   1. Bunga(Rp) =( Modal x Waktu x Bunga(%) ) / 100
   2. Waktu (tahun) = Bunga yang diterima / Bunga dalam setahun
   3. Modal =( Bunga(Rp) x 100 )/ (Waktu x Bunga(%) )
Bunga (dalam %) =(bunga setahun / modal) x 100%

Valenta's World

Minggu, 21 Februari 2016

Ringkasan Matematika kelas 9 semester 1

Bab 1: Bilangan Berpangkat dan bentuk akar

_{Bab 2: Pola ,Barisan,dan Deret}

Bab 3 : Perbandingan Bertingkat

Persentase Untung Rugi

Tidak ada komentar:

Posting Komentar

Arsip Blog